【论文】Towards Deep Learning Models Resistant to Adversarial Attacks

论文题目：【论文】Towards Deep Learning Models Resistant to Adversarial Attacks

作者：Aleksander Madry，Aleksandar Makelov，Ludwig Schmidt，Dimitris Tsipras，Adrian Vladu

会议/时间：ICLR2018

链接: arXiv

论文目标

很多模型对 Adversarial Examples 对抗样本 比较敏感，特别是计算机视觉任务中，输入图片添加微小扰动就可能使模型输出错误的结果。文章中通过对抗训练的方式得到一个对对抗样本不敏感的模型，从而使得模型具有较高的鲁棒性。

相关工作

现有的对抗样本算法，主要专注解决两个问题，一个是如何用更小的扰动对结果造成更大的影响，另一个是如何训练一个鲁棒性较强的模型，或者是对抗样本较难获得的模型。

对抗样本的生成方面，主要是 FGSM 快速梯度下降法 算法及其各种变种，以及 PGD 算法。

在防御端，主要是采用 Adversarial Training 对抗训练 的思路，利用FGSM生成的对抗样本参与训练。

本文方法

考虑到对抗样本攻击通常在输入数据上添加一个扰动，因此针对对抗样本提高模型鲁棒性的方式可以表示为一个 Min-Max优化问题 ，或者称为 对抗优化 问题，表示如下。其中$L(\theta, x, y)$为经验损失。

$$ \min_{\theta} \rho(\theta), where\quad \rho(\theta) = \mathbb{E}_{(x,y)\sim \mathcal{D}}\left[\max_{\delta \in S} L(\theta,x+\delta,y) \right] $$

解决这样的对抗优化问题需要解决非凸的优化问题，包括内部的最大化问题和外部的最小化问题。

文中通过实验发现，在选定数据的 $l_{\infty}-Ball$内部（参考 无穷范数 ）存在非常多的局部最优点，并且具有很小的损失值。在实验中通过使用 PGD 算法 生成对抗数据并测试可以得到，PGD可以作为一种通用的攻击方式，在选定数据附近得到一个局部最优。因此能对抗PGD的算法也能比较好的对抗一阶攻击（First-Order Adversarial，只利用一阶梯度值生成对抗样本的攻击）。因此使用PGD生成的对抗样本作为内部最大化问题的解。

对于外部的最小化问题，可以直接使用SGD优化器进行优化，即计算 $\nabla_{\theta}\ \rho(\theta)$。假设Danskin’s定理在当前问题上成立，可推出可以使用SGD优化器优化外部最小化问题求解，实验结果也证明这一点。

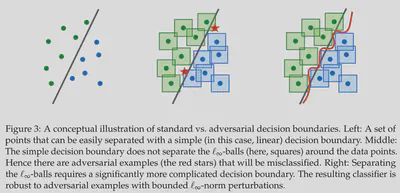
上图说明，对于使用对抗训练的模型，由于模型对于数据的微小扰动不敏感，模型就需要学习到更加复杂的决策边界，这也需要模型具有更大的 模型容量|容量 。因此需要换用容量更大更复杂的模型。

结果分析

使用不同的对抗样本进行对抗训练并测试的结果如下，一方面增加模型容量能提升对抗攻击下的模型性能，使得最终学到的损失函数鞍点更小，另一方面使用PGD 算法作为对抗目标的效果比使用FGSM 快速梯度下降法更好。

总结

通过对抗样本参与训练可以增强模型的鲁棒性。