【论文】Non-local Neural Networks
论文题目:Non-local Neural Networks
作者:Xiaolong Wang, Ross Girshick, Abhinav Gupta, Kaiming He
会议/时间:CVPR2018
链接:https://arxiv.org/abs/1711.07971
论文目标
当前的CNN或者RNN结构中的卷积等操作都是针对数据中的一个小区域(local neighborhood)处理和提取特征,并没有考虑到数据中的长期/远距离依赖关系。因此设计一个non-local操作,可以考虑到输入数据中的每一个位置上的特征和依赖关系,学习到全局信息。
相关工作
在CNN中通过多次卷积扩大感受野,在RNN中通过设计迭代模型学习到序列中的远距离特征/信息,但是在实际的每一次处理过程中都只考虑到局部的信息。通过重复处理局部信息获得全局信息不仅计算效率低,而且引入了优化的困难。
参考了传统的CV领域使用的non-local mean operation方法。其他相关的内容包括Graphical models、Feedforward modeling for sequences、self-attention、interaction networks、video classification architectures等。实际上self-attention可以看作是non-local的一种情况。
本文思路/解决方案
通过考虑特征图中每一个位置的加权和来得到特定位置的响应。
一方面可以直接学习到数据中远距离的信息,另一方面使用较浅层的网络也能实现比较好的结果,而且作者设计的non-local模块不改变数据的大小,可以方便的插在现有的网络中。
简单来说,non-local的思路如下,其中$x_i$为输出位置,$x_j$为数据中的每一个点,使用$f(x_i,x_j)$计算两者之间的关系并作为权重计算输入数据特征$g(x)$的加权和。
$$ y_i = \frac{1}{C(x)}\sum\limits_{\forall j}f(x_i, x_j)g(x_j) $$在实际使用过程中,函数$f(\cdot)$和$g(\cdot)$有多种选择。后者常选用$1\times1\times1$的卷积实现。
| Function Type | Pairwise Function |
|---|---|
| Gaussian | $f(x_i,x_j) = e^{x_i^T x_j}$ |
| Embedded Gaussian | $f(x_i, x_j) =e^{\theta(x_i)^T\phi(x_j)}$ |
| Dot product | $f(x_i,x_j) = \theta(x_i)^T\phi(x_j)$ |
| Concatenation | $f(x_i, x_j) = ReLU(w_f^T[\theta(x_i),\phi(x_j)])$ 其中$[\cdot, \cdot]$表示连接得向量并经$w_f$变成标量 |
通过将non-local block定义为残差结构,使得模块输出的形状不发生变化,可以将non-local block插入到已有的预训练模型中,而不改变其性能($W_z$初始化为0)。通过在较高的特征层加入该block,同时引入降采样,可以减小引入的计算量。
$$ z_i = W_z y_i + x_i $$
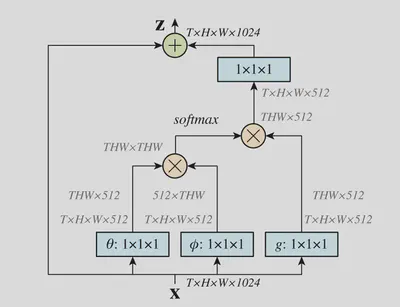
结果
经过测试,添加了non-local block的模型具有更高的预测准确率,在non-local block中选择不同的函数计算数据之间的距离(即$f(x_i,x_j)$)对于最后的模型效果影响不大。而且在模型中添加了时空维度上的nonn-local block后效果相比单纯的时间或空间维度的效果更好。
总结
提出了一种non-local的结构学习数据中距离比较远的特征的影响。并且实现了一种non-local block可以插入到现有的网络结构中并提升其性能。