【论文】Embedding Watermarks into Deep Neural Networks

论文题目： Embedding Watermarks into Deep Neural Networks

作者： Yusuke Uchida, Yuki Nagai, Shigeyuki Sakazawa

会议/时间：ICMR 2017

链接: arXiv

论文目标

目前预训练深度神经网络的应用越来越广，需要一种数字水印技术来保护预训练深度神经网络的知识产权，避免被滥用。论文首先定义了水印技术的场景，并提出了一种水印嵌入技术，可以在模型训练、精调或者蒸馏过程中嵌入到目标模型中且不影响模型性能。并且面对攻击者的精调和剪枝等行为时仍能保留在模型中。

问题定义

模型水印要求

要求	解释
Fidelity	添加水印之后模型的性能没有明显下降
Robustness	模型经过修改后水印仍存在
Capacity	水印技术应该能够嵌入大量信息
Security	水印应该难以被他人读写和修改
Efficiency	嵌入和提取水印的过程应该足够快

模型水印嵌入方法

1. 在训练过程中嵌入（Train From Scratch）
2. 在精调过程中嵌入（Fine-Tuning）
3. 在蒸馏过程中嵌入（Model Distillation）

攻击方法

1. 精调（Fine Tuning）
2. 模型压缩（Model Compression）

本文方法

主要考虑卷积神经网络中卷积层的参数。对于一个$Kernel-Size=S$，输入通道数为$D$，输出通道数（卷积核数量）为$L$的卷积层，不考虑偏置，其参数为$W \in \mathbb{R}^{S\times S\times D\times L}$。计算多个卷积核的均值 $ {\bar W}_{i,j,k}=\frac{1}{L}\sum_l W_{i,j,k,l} $，并展平得到$w \in \mathbb{R}^M(M = S\times S\times D)$作为嵌入的目标。将$T$-bit的信息$b\in {0,1}^T$嵌入其中。

在提取时，使用$b_j = s(\sum_i X_{ji}\omega_i)$计算嵌入的信息。其中$\omega$表示卷积核均值，$X \in \mathbb{R}^{T \times M}$表示嵌入密钥，$s(\cdot)$为阶跃函数。

在训练时，为了将信息嵌入模型中，在原本的损失函数上添加了一个权重参数正则项$E(\omega)=E_0(\omega)+\lambda E_R(\omega)$。

考虑到上述的模型提取方式类似二分类方法，因此添加的权重参数正则项使用BCE损失，使用训练过程中的参数提取结果作为监督。

$$\begin{aligned} E_R(\omega)=& -\sum\limits_{j=1}^{T}(b_j \log(y_j)+(1-b_j)\log(1-y_j)) \\ y_j =& \sigma(\sum_i X_{ji}\omega_i)\\ \sigma(x) =& \frac{1}{1+\exp(-x)} \end{aligned}$$

关于密钥$X$的设计，考虑到水印的性能，有三种设计形式：$X^{direct}$的每一行为独热码，直接将信息映射到参数中。$X^{diff}$的每一行包含一个1和一个-1，其他的为0，将信息映射到参数的差值中。$X^{random}$的数字采样于标准正态分布。

结果分析

Ablation Study

关于密钥$W$的设计，实验证明使用$X^{direct}$和$X^{diff}$嵌入都会造成较大的性能下降。

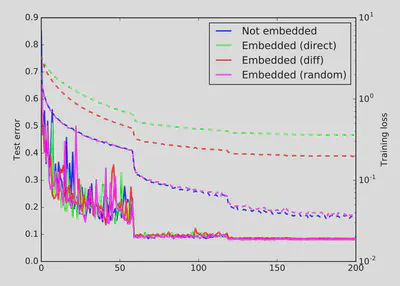
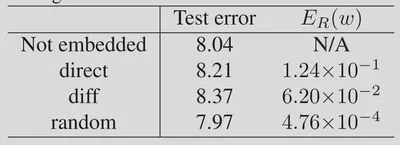
而且可以看到$X^{random}$不仅不造成性能下降，而且对原始的参数分布影响不大。

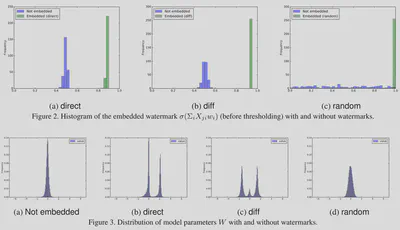
经过实验发现，当嵌入的信息量超过卷积层参数数量的时候，嵌入损失和性能下降会变得明显。而且采用直接嵌入的方式会难以在性能下降和嵌入损失之间达到均衡。

Robustness

实验证实这一方法可以应对Fine-Tuning和迁移学习。

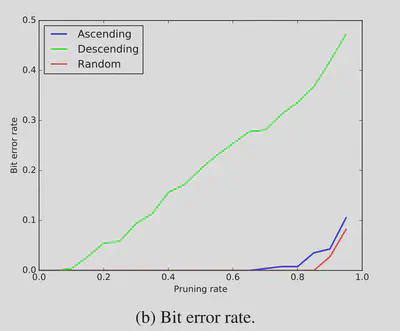
面对剪枝操作时，特别是按照权重升序的剪枝方法时仍然能保留水印。

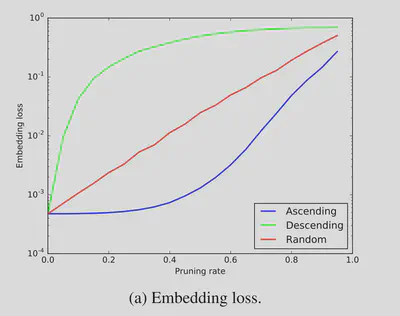
总结

提出了一种，为权重参数添加正则项的水印嵌入方法，其水印提取是通过矩阵映射的方式实现的。具有一定的鲁棒性。